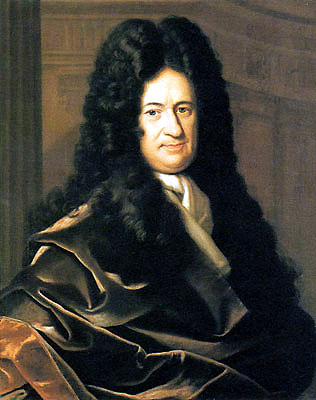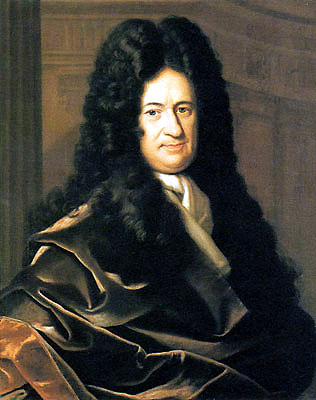
Signature
Full name
Gottfried Wilhelm Leibniz
Birth1 July (21 June Old Style) 1646,
Leipzig,
Electorate of SaxonyDeath
14 November 1716, Hanover, Electorate of Hanover
School/traditionRationalismMain interests
Metaphysics,
Mathematics,
TheodicyNotable ideasInfinitesimal calculus,
Calculus,
Monadology,
Theodicy,
Optimism Gottfried Wilhelm Leibniz (pronounced
[ˈlaɪpnɪts]; also Leibnitz or von Leibniz; 1 July 1646 [
OS: 21 June] – 14 November 1716) was a
German polymath who wrote primarily in
Latin and French.
He occupies an equally grand place in both the
history of philosophy and the
history of mathematics. He invented
infinitesimal calculus independently of
Newton, and his
notation is the one in general use since then. He also invented the
binary system, foundation of virtually all modern computer architectures. In philosophy, he is mostly remembered for
optimism, i.e. his conclusion that our universe is, in a restricted sense, the best possible one
God could have made. He was, along with
René Descartes and
Baruch Spinoza, one of the three greatest 17th-century
rationalists, but his philosophy also looks back to the
scholastic tradition and anticipates modern
logic and
analysis. Leibniz also made major contributions to
physics and
technology, and anticipated notions that surfaced much later in
biology,
medicine,
geology,
probability theory,
psychology,
linguistics, and
information science. He also wrote on
politics,
law,
ethics,
theology,
history, and
philology, even occasional verse. His contributions to this vast array of subjects are scattered in journals and in tens of thousands of letters and unpublished manuscripts. As of 2008, there is no complete edition of Leibniz's writings.
Biography
Early life
Gottfried Leibniz was born on 1 July 1646 in
Leipzig to Friedrich Leibniz and Catherina Schmuck. His father passed away when he was six, so he learned his religious and moral values from his mother. These would exert a profound influence on his philosophical thought in later life. As an adult, he often styled himself "von Leibniz", and many posthumous editions of his works gave his name on the title page as "Freiherr [Baron] G. W. von Leibniz." However, no document has been found confirming that he was ever granted a patent of nobility.
[2]When Leibniz was six years old, his father, a Professor of Moral Philosophy at the
University of Leipzig, died, leaving a personal library to which Leibniz was granted free access from age seven onwards. By 12, he had taught himself
Latin, which he used freely all his life, and had begun studying
Greek.
He entered his father's university at age 14, and completed university studies by 20, specializing in law and mastering the standard university courses in classics, logic, and scholastic philosophy. However, his education in mathematics was not up to the French and British standards. In 1666 (age 20), he published his first book, also his
habilitation thesis in philosophy,
On the Art of Combinations. When
Leipzig declined to assure him a position teaching law upon graduation, Leibniz submitted the thesis he had intended to submit at Leipzig to the
University of Altdorf instead, and obtained his doctorate in law in five months. He then declined an offer of academic appointment at Altdorf, and spent the rest of his life in the service of two major German noble families.
1666–74Leibniz's first position was as a salaried alchemist in
Nuremberg, even though he knew nothing about the subject. He soon met Johann Christian von Boineburg (1622–1672), the dismissed chief minister of the Elector of
Mainz,
Johann Philipp von Schönborn. Von Boineburg hired Leibniz as an assistant, and shortly thereafter reconciled with the Elector and introduced Leibniz to him. Leibniz then dedicated an essay on law to the Elector in the hope of obtaining employment. The stratagem worked; the Elector asked Leibniz to assist with the redrafting of the legal code for his Electorate. In 1669, Leibniz was appointed Assessor in the Court of Appeal. Although von Boineburg died late in 1672, Leibniz remained under the employment of his widow until she dismissed him in 1674.
Von Boineburg did much to promote Leibniz's reputation, and the latter's memoranda and letters began to attract favorable notice. Leibniz's service to the Elector soon followed a
diplomatic role. He published an essay, under the pseudonym of a fictitious
Polish nobleman, arguing (unsuccessfully) for the German candidate for the Polish crown. The main European geopolitical reality during Leibniz's adult life was the ambition of
Louis XIV of France, backed by French military and economic might. Meanwhile, the
Thirty Years' War had left German-speaking Europe exhausted, fragmented, and economically backward. Leibniz proposed to protect German-speaking Europe by distracting Louis as follows. France would be invited to take
Egypt as a stepping stone towards an eventual conquest of the
Dutch East Indies. In return, France would agree to leave Germany and the Netherlands undisturbed. This plan obtained the Elector's cautious support. In 1672, the French government invited Leibniz to
Paris for discussion, but the plan was soon overtaken by events and became irrelevant. Napoleon's failed invasion of Egypt in 1798 can be seen as an unwitting implementation of Leibniz's plan.
Thus Leibniz began several years in Paris. Soon after arriving, he met
Dutch physicist and mathematician
Christiaan Huygens and realised that his own knowledge of mathematics and physics was spotty. With Huygens as mentor, he began a program of self-study that soon pushed him to making major contributions to both subjects, including inventing his version of the differential and integral
calculus. He met
Malebranche and
Antoine Arnauld, the leading French philosophers of the day, and studied the writings of
Descartes and
Pascal, unpublished as well as published. He befriended a German mathematician,
Ehrenfried Walther von Tschirnhaus; they corresponded for the rest of their lives.
When it became clear that France would not implement its part of Leibniz's Egyptian plan, the Elector sent his nephew, escorted by Leibniz, on a related mission to the English government in
London, early in 1673. There Leibniz came into acquaintance of
Henry Oldenburg and
John Collins. After demonstrating a calculating machine to the
Royal Society he had been designing and building since 1670, the first such machine that could execute all four basic arithmetical operations, the Society made him an external member. The mission ended abruptly when news reached it of the Elector's death, whereupon Leibniz promptly returned to Paris and not, as had been planned, to Mainz.
The sudden deaths of Leibniz's two patrons in the same winter meant that Leibniz had to find a new basis for his career. In this regard, a 1669 invitation from the Duke of
Brunswick to visit Hanover proved fateful. Leibniz declined the invitation, but began corresponding with the Duke in 1671. In 1673,
the Duke offered him the post of Counsellor which Leibniz very reluctantly accepted two years later, only after it became clear that no employment in Paris, whose intellectual stimulation he relished, or with the
Habsburg imperial court was forthcoming.
House of Hanover, 1676–1716Leibniz managed to delay his arrival in Hanover until the end of 1676, after making one more short journey to London, where he possibly was shown some of Newton's unpublished work on the calculus. This fact was deemed evidence supporting the accusation, made decades later, that he had stolen the calculus from Newton. On the journey from London to Hanover, Leibniz stopped in
The Hague where he met
Leeuwenhoek, the discoverer of microorganisms. He also spent several days in intense discussion with
Spinoza, who had just completed his masterwork, the
Ethics. Leibniz respected Spinoza's powerful intellect, but was dismayed by his conclusions that contradicted both Christian and Jewish orthodoxy.
In 1677, he was promoted, at his request, to Privy Counselor of Justice, a post he held for the rest of his life. Leibniz served three consecutive rulers of the House of Brunswick as historian, political adviser, and most consequentially, as librarian of the
ducal library. He thenceforth employed his pen on all the various political, historical, and
theological matters involving the House of Brunswick; the resulting documents form a valuable part of the historical record for the period.
Among the few people in north Germany to warm to Leibniz were the Electress
Sophia of Hanover (1630–1714), her daughter
Sophia Charlotte of Hanover (1668–1705), the Queen of Prussia and her avowed disciple, and
Caroline of Ansbach, the consort of her grandson, the future
George II. To each of these women he was correspondent, adviser, and friend. In turn, they all warmed to him more than did their spouses and the future king
George I of Great Britain.
[3]The population of Hanover was only about 10,000, and its provinciality eventually grated on Leibniz. Nevertheless, to be a major courtier to the House of
Brunswick was quite an honor, especially in light of the meteoric rise in the prestige of that House during Leibniz's association with it. In 1692, the Duke of Brunswick became a hereditary Elector of the
Holy Roman Empire. The British
Act of Settlement 1701 designated the Electress Sophia and her descent as the royal family of the United Kingdom, once both King
William III and his sister-in-law and successor,
Queen Anne, were dead. Leibniz played a role in the initiatives and negotiations leading up to that Act, but not always an effective one. For example, something he published anonymously in England, thinking to promote the Brunswick cause, was formally censured by the
British Parliament.
The Brunswicks tolerated the enormous effort Leibniz devoted to intellectual pursuits unrelated to his duties as a courtier, pursuits such as perfecting the calculus, writing about other mathematics, logic, physics, and philosophy, and keeping up a vast correspondence. He began working on the calculus in 1674; the earliest evidence of its use in his surviving notebooks is 1675. By 1677 he had a coherent system in hand, but did not publish it until 1684. Leibniz's most important mathematical papers were published between 1682 and 1692, usually in a journal which he and Otto Mencke founded in 1682, the
Acta Eruditorum. That journal played a key role in advancing his mathematical and scientific reputation, which in turn enhanced his eminence in diplomacy, history, theology, and philosophy.
The Elector
Ernst August commissioned Leibniz to write a history of the House of
Brunswick, going back to the time of
Charlemagne or earlier, hoping that the resulting book would advance his dynastic ambitions. From 1687 to 1690, Leibniz traveled extensively in Germany, Austria, and Italy, seeking and finding archival materials bearing on this project. Decades went by but no history appeared; the next Elector became quite annoyed at Leibniz's apparent dilatoriness. Leibniz never finished the project, in part because of his huge output on many other fronts, but also because he insisted on writing a meticulously researched and erudite book based on archival sources, when his patrons would have been quite happy with a short popular book, one perhaps little more than a
genealogy with commentary, to be completed in three years or less. They never knew that he had in fact carried out a fair part of his assigned task: when the material Leibniz had written and collected for his history of the House of Brunswick was finally published in the 19th century, it filled three volumes.
In 1711, John Keill, writing in the journal of the Royal Society and with Newton's presumed blessing, accused Leibniz of having plagiarized Newton's calculus. Thus began the
calculus priority dispute which darkened the remainder of Leibniz's life. A formal investigation by the Royal Society (in which Newton was an unacknowledged participant), undertaken in response to Leibniz's demand for a retraction, upheld Keill's charge. Historians of mathematics writing since 1900 or so have tended to acquit Leibniz, pointing to important differences between Leibniz's and Newton's versions of the calculus.
In 1711, while traveling in northern Europe, the Russian
Tsar Peter the Great stopped in Hanover and met Leibniz, who then took some interest in matters Russian over the rest of his life. In 1712, Leibniz began a two year residence in
Vienna, where he was appointed Imperial Court Councillor to the
Habsburgs. On the death of Queen Anne in 1714, Elector Georg Ludwig became King
George I of Great Britain, under the terms of the 1701
Act of Settlement. Even though Leibniz had done much to bring about this happy event, it was not to be his hour of glory. Despite the intercession of the Princess of Wales,
Caroline of Ansbach, George I forbade Leibniz to join him in London until he completed at least one volume of the history of the Brunswick family his father had commissioned nearly 30 years earlier. Moreover, for George I to include Leibniz in his London court would have been deemed insulting to Newton, who was seen as having won the calculus priority dispute and whose standing in British official circles could not have been higher. Finally, his dear friend and defender, the dowager Electress
Sophia, died in 1714.
Leibniz died in
Hanover in 1716: at the time, he was so out of favor that neither George I (who happened to be near Hanover at the time) nor any fellow courtier other than his personal secretary attended the funeral. Even though Leibniz was a life member of the Royal Society and the
Berlin Academy of Sciences, neither organization saw fit to honor his passing. His grave went unmarked for more than 50 years. Leibniz was eulogized by
Fontenelle, before the Academie des Sciences in Paris, which had admitted him as a foreign member in 1700. The eulogy was composed at the behest of the
Duchess of Orleans, a niece of the Electress Sophia.
Leibniz never married. He complained on occasion about money, but the fair sum he left to his sole heir, his sister's stepson, proved that the Brunswicks had, by and large, paid him well. In his diplomatic endeavors, he at times verged on the unscrupulous, as was all too often the case with professional diplomats of his day. On several occasions, Leibniz backdated and altered personal manuscripts, actions which cannot be excused or defended and which put him in a bad light during the calculus controversy. On the other hand, he was charming, well-mannered, and not without humor and imagination;
[4] he had many friends and admirers all over Europe.
Philosopher
Leibniz's philosophical thinking appears fragmented, because his philosophical writings consist mainly of a multitude of short pieces: journal articles, manuscripts published long after his death, and many letters to many correspondents. He wrote only two philosophical treatises, and the one he published in his lifetime, the Théodicée of 1710, is as much theological as philosophical.
Leibniz dated his beginning as a philosopher to his
Discourse on Metaphysics, which he composed in 1686 as a commentary on a running dispute between
Malebranche and
Antoine Arnauld. This led to an extensive and valuable correspondence with Arnauld;
[5] it and the Discourse were not published until the 19th century. In 1695, Leibniz made his public entrée into European philosophy with a journal article titled "New System of the Nature and Communication of Substances".
[6] Between 1695 and 1705, he composed his
New Essays on Human Understanding, a lengthy commentary on
John Locke's 1690
An Essay Concerning Human Understanding, but upon learning of Locke's 1704 death, lost the desire to publish it, so that the New Essays were not published until 1765. The
Monadologie, composed in 1714 and published posthumously, consists of 90 aphorisms.
Leibniz met
Spinoza in 1676, read some of his unpublished writings, and has since been suspected of appropriating some of Spinoza's ideas. While Leibniz admired Spinoza's powerful intellect, he was also forthrightly dismayed by Spinoza's conclusions,
[7] especially when these were inconsistent with Christian orthodoxy.
Unlike Descartes and Spinoza, Leibniz had a thorough university education in philosophy. His lifelong
scholastic and
Aristotelian turn of mind betrayed the strong influence of one of his
Leipzig professors,
Jakob Thomasius, who also supervised his BA thesis in philosophy. Leibniz also eagerly read
Francisco Suárez, a Spanish
Jesuit respected even in
Lutheran universities. Leibniz was deeply interested in the new methods and conclusions of Descartes, Huygens, Newton, and
Boyle, but viewed their work through a lens heavily tinted by scholastic notions. Yet it remains the case that Leibniz's methods and concerns often anticipate the
logic, and
analytic and
linguistic philosophy of the 20th century.
Leibniz variously invoked one or another of seven fundamental philosophical Principles:
[8]Identity/
contradiction. If a proposition is true, then its negation is false and vice versa.
Identity of indiscernibles. Two things are identical if and only if they share the same properties. Frequently invoked in modern logic and philosophy. The "identity of indiscernibles" is often referred to as Leibniz's Law. It has attracted the most controversy and criticism, especially from corpuscular philosophy and quantum mechanics.
Sufficient reason. "There must be a sufficient reason [often known only to God] for anything to exist, for any event to occur, for any truth to obtain."
[9]Pre-established harmony.
[10] "[T]he appropriate nature of each substance brings it about that what happens to one corresponds to what happens to all the others, without, however, their acting upon one another directly." (Discourse on Metaphysics, XIV) A dropped glass shatters because it "knows" it has hit the ground, and not because the impact with the ground "compels" the glass to split.
Continuity. Natura non saltum facit. A mathematical analog to this principle would proceed as follows. If a
function describes a
transformation of something to which continuity applies, then its
domain and
range are both
dense sets.
Optimism. "God assuredly always chooses the best."
[11]Plenitude. "Leibniz believed that the best of all possible worlds would actualize every genuine possibility, and argued in
Théodicée that this best of all possible worlds will contain all possibilities, with our finite experience of eternity giving no reason to dispute nature's perfection."
Leibniz would on occasion give a speech for a specific principle, but more often took them for granted.
[12]Leibniz's best known contribution to
metaphysics is his theory of
monads, as exposited in
Monadologie. Monads are to the metaphysical realm what
atoms are to the physical/phenomenal. Monads are the ultimate elements of the
universe. The monads are "substantial forms of being" with the following properties: they are eternal, indecomposable, individual, subject to their own laws, un-interacting, and each reflecting the entire universe in a
pre-established harmony (a historically important example of
panpsychism). Monads are centers of
force; substance is force, while
space,
matter, and
motion are merely phenomenal.
The
ontological essence of a monad is its irreducible simplicity. Unlike atoms, monads possess no material or spatial character. They also differ from atoms by their complete mutual independence, so that interactions among monads are only apparent. Instead, by virtue of the principle of pre-established harmony, each monad follows a preprogrammed set of "instructions" peculiar to itself, so that a monad "knows" what to do at each moment. (These "instructions" may be seen as analogs of the
scientific laws governing
subatomic particles.) By virtue of these intrinsic instructions, each monad is like a little mirror of the universe. Monads need not be "small"; e.g., each human being constitutes a monad, in which case
free will is problematic.
God, too, is a monad, and the
existence of God can be inferred from the harmony prevailing among all other monads; God wills the pre-established harmony.
Monads are purported to having gotten rid of the problematic:
Interaction between
mind and
matter arising in the system of
Descartes;
Lack of
individuation inherent to the system of
Spinoza, which represents individual creatures as merely
accidental.
The monadology was thought arbitrary, even eccentric, in Leibniz's day and since.
Theodicy and optimism
The
Théodicée[13] tries to justify the apparent imperfections of the world by claiming that it is
optimal among all possible worlds. It must be the best possible and most balanced world, because it was created by a perfect God.
The statement that "we live in the best of all possible worlds" drew scorn, most notably from
Voltaire, who lampooned it in his comic novella
Candide by having the character Dr. Pangloss (a parody of Leibniz) repeat it like a
mantra. Thus the adjective "
panglossian", which describes one who believes that the world about us is the best possible one.
The mathematician
Paul du Bois-Reymond, in his "Leibnizian Thoughts in Modern Science", wrote that Leibniz thought of God as a
mathematician:
As is well known, the theory of the
maxima and minima of
functions was indebted to him for the greatest progress through the discovery of the method of
tangents. Well, he conceives God in the creation of the world like a mathematician who is solving a minimum problem, or rather, in our modern phraseology, a problem in the
calculus of variations – the question being to determine among an infinite number of possible worlds, that for which the sum of necessary evil is a minimum.
A cautious defense of Leibnizian optimism would invoke certain scientific principles that emerged in the two centuries since his death and that are now thoroughly established: the
principle of least action, the
conservation of mass, and the
conservation of energy. In addition, the modern observations that lead to the
Fine-tuned Universe arguments seem to support his view:
The 3+1 dimensional structure of
spacetime may be ideal. In order to sustain
complexity such as
life, a
universe probably requires three
spatial and one
temporal dimension. Most universes deviating from 3+1 either violate some fundamental
physical laws, or are impossible. The mathematically richest number of spatial dimensions is also 3 (in the sense of topological nontriviality).
The
universe,
solar system, and
Earth are the "best possible" in that they enable intelligent life to exist. Such life exists on Earth only because the
Earth,
solar system, and
Milky Way possess a number of unusual characteristics.
[14]The most sweeping form of
optimism derives from the
Anthropic Principle.
[15] Physical reality can be seen as grounded in the numerical values of a handful of
dimensionless constants, the best known of which are the
fine structure constant and the ratio of the
rest mass of the
proton to the
electron. Were the numerical values of these constants to differ by a few percent from their observed values, it is unlikely that the resulting universe would contain
complex structures.
Our
physical laws,
universe,
solar system, and
home planet are all "best" in the sense that they enable
complex structures such as
galaxies,
stars, and, ultimately,
intelligent life. On the other hand, it is also reasonable to believe that life might be more intelligent given some other set of circumstances.
Symbolic thought
Leibniz believed that much of human reasoning could be reduced to calculations of a sort, and that such calculations could resolve many differences of opinion:
The only way to rectify our reasonings is to make them as tangible as those of the Mathematicians, so that we can find our error at a glance, and when there are disputes among persons, we can simply say: Let us calculate [calculemus], without further ado, to see who is right.
[16]Leibniz's
calculus ratiocinator, which resembles
symbolic logic, can be viewed as a way of making such calculations feasible. Leibniz wrote memoranda
[17] that can now be read as groping attempts to get symbolic logic—and thus his calculus—off the ground. But Gerhard and Couturat did not publish these writings until modern formal logic had emerged in
Frege's Begriffsschrift and in writings by
Charles Peirce and his students in the 1880s, and hence well after
Boole and
De Morgan began that logic in 1847.
Leibniz thought
symbols were important for human understanding. He attached so much importance to the invention of good notations that he attributed all his discoveries in mathematics to this. His notation for the
infinitesimal calculus is an example of his skill in this regard.
Charles Peirce, a 19th-century pioneer of
semiotics, shared Leibniz's passion for symbols and notation, and his belief that these are essential to a well-running logic and mathematics.
But Leibniz took his speculations much further. Defining a
character as any written sign, he then defined a "real" character as one that represents an idea directly and not simply as the word embodying the idea. Some real characters, such as the notation of logic, serve only to facilitate reasoning. Many characters well-known in his day, including
Egyptian hieroglyphics,
Chinese characters, and the symbols of
astronomy and
chemistry, he deemed not real.
[18] Instead, he proposed the creation of a
characteristica universalis or "universal characteristic", built on an
alphabet of human thought in which each fundamental concept would be represented by a unique "real" character:
It is obvious that if we could find characters or signs suited for expressing all our thoughts as clearly and as exactly as arithmetic expresses numbers or geometry expresses lines, we could do in all matters insofar as they are subject to reasoning all that we can do in arithmetic and geometry. For all investigations which depend on reasoning would be carried out by transposing these characters and by a species of calculus.
[19]Complex thoughts would be represented by combining characters for simpler thoughts. Leibniz saw that the uniqueness of
prime factorization suggests a central role for
prime numbers in the universal characteristic, a striking anticipation of
Gödel numbering. Granted, there is no intuitive or
mnemonic way to number any set of elementary concepts using the prime numbers.
Because Leibniz was a mathematical novice when he first wrote about the characteristic, at first he did not conceive it as an
algebra but rather as a
universal language or script. Only in 1676 did he conceive of a kind of "algebra of thought", modeled on and including conventional algebra and its notation. The resulting characteristic included a logical calculus, some combinatorics, algebra, his analysis situs (geometry of situation), a universal concept language, and more.
What Leibniz actually intended by his
characteristica universalis and
calculus ratiocinator, and the extent to which modern formal logic does justice to the calculus, may never be established.
[20]Formal logic
Main article:
algebraic logicLeibniz is the most important logician between Aristotle and 1847, when
George Boole and
Augustus De Morgan each published books that began modern formal logic. Leibniz enunciated the principal properties of what we now call
conjunction,
disjunction,
negation,
identity, set
inclusion, and the
empty set. The principles of Leibniz's logic and, arguably, of his whole philosophy, reduce to two:
All our ideas are compounded from a very small number of simple ideas, which form the
alphabet of human thought.
Complex ideas proceed from these simple ideas by a uniform and symmetrical combination, analogous to arithmetical multiplication.
With regard to the first point, the number of simple ideas is much greater than Leibniz thought. As for the second, logic can indeed be grounded in a symmetrical combining operation, but that operation is analogous to either of addition or multiplication. The formal logic that emerged early in the 20th century also requires, at minimum, unary
negation and
quantified variables ranging over some
universe of discourse.
Leibniz published nothing on formal logic in his lifetime; most of what he wrote on the subject consists of working drafts. In his book
History of Western Philosophy,
Bertrand Russell went so far as to claim that Leibniz had developed logic in his unpublished writings to a level which was reached only 200 years later.
Mathematician
Although the mathematical notion of
function was implicit in trigonometric and logarithmic tables, which existed in his day, Leibniz was the first, in 1692 and 1694, to employ it explicitly, to denote any of several geometric concepts derived from a curve, such as
abscissa,
ordinate,
tangent,
chord, and the
perpendicular.
[21] In the 18th century, "function" lost these geometrical associations.
Leibniz was the first to see that the coefficients of a system of
linear equations could be arranged into an array, now called a
matrix, which can be manipulated to find the solution of the system, if any. This method was later called
Gaussian elimination. Leibniz's discoveries of
Boolean algebra and of
symbolic logic, also relevant to mathematics, are discussed in the preceding section. A comprehensive scholarly treatment of Leibniz's mathematical writings has yet to be written.
Calculus
Leibniz is credited, along with
Isaac Newton, with the discovery of
infinitesimal calculus. According to Leibniz's notebooks, a critical breakthrough occurred on 11 November 1675, when he employed integral calculus for the first time to find the area under the function y = x. He introduced several notations used to this day, for instance the
integral sign ∫ representing an elongated S, from the Latin word summa and the d used for
differentials, from the Latin word differentia. This ingenious and suggestive notation for the calculus is probably his most enduring mathematical legacy. Leibniz did not publish anything about his calculus until 1684.
[22] The
product rule of
differential calculus is still called "Leibniz's law". In addition, the theorem that tells how and when to differentiate under the integral sign is called the
Leibniz integral rule.
Leibniz's approach to the calculus fell well short of later standards of rigor (the same can be said of Newton's). We now see a Leibniz "proof" as being in truth mostly a
heuristic hodgepodge mainly grounded in geometric intuition. Leibniz also freely invoked mathematical entities he called
infinitesimals, manipulating them in ways suggesting that they had
paradoxical algebraic properties.
George Berkeley, in a tract called The Analyst and elsewhere[
citation needed], ridiculed this and other aspects of the early calculus, pointing out that natural science grounded in the calculus required just as big of a leap of
faith as
theology grounded in
Christian revelation.
From 1711 until his death, Leibniz's life was envenomed by
a long dispute with John Keill, Newton, and others, over whether Leibniz had invented the calculus independently of Newton, or whether he had merely invented another notation for ideas that were fundamentally Newton's.
[23]Modern, rigorous calculus emerged in the 19th century, thanks to the efforts of
Augustin Louis Cauchy,
Bernhard Riemann,
Karl Weierstrass, and others, who based their work on the definition of a
limit and on a precise understanding of
real numbers. Their work discredited the use of
infinitesimals to justify calculus. Yet, infinitesimals survived in science and engineering, and even in rigorous mathematics, via the fundamental computational device known as the
differential. Beginning in 1960,
Abraham Robinson worked out a rigorous foundation for Leibniz's infinitesimals, using
model theory. The resulting
nonstandard analysis can be seen as a belated vindication of Leibniz's mathematical reasoning.
Topology
Leibniz was the first to use the term analysis situs,
[24] later used in the 19th century to refer to what is now known as
topology. There are two takes on this situation. On the one hand, Mates, citing a 1954 paper in German by
Jacob Freudenthal, argues:
Although for [Leibniz] the situs of a sequence of points is completely determined by the distance between them and is altered if those distances are altered, his admirer
Euler, in the famous 1736 paper solving the
Königsberg Bridge Problem and its generalizations, used the term geometria situs in such a sense that the situs remains unchanged under topological deformations. He mistakenly credits Leibniz with originating this concept. ...it is sometimes not realized that Leibniz used the term in an entirely different sense and hence can hardly be considered the founder of that part of mathematics.
[25]But Hirano argues differently, quoting Mandelbrot:
To sample Leibniz' scientific works is a sobering experience. Next to calculus, and to other thoughts that have been carried out to completion, the number and variety of premonitory thrusts is overwhelming. We saw examples in 'packing,'... My Leibniz mania is further reinforced by finding that for one moment its hero attached importance to geometric scaling. In "Euclidis Prota"..., which is an attempt to tighten Euclid's axioms, he states,...: 'I have diverse definitions for the straight line. The straight line is a curve, any part of which is similar to the whole, and it alone has this property, not only among curves but among sets.' This claim can be proved today.
[26]Thus the fractal geometry promoted by Mandelbrot drew on Leibniz's notions of self-similarity and the principle of continuity: natura non facit saltus. We also see that when Leibniz wrote, in a metaphysical vein, that "the straight line is a curve, any part of which is similar to the whole", he was anticipating topology by more than two centuries. As for "packing", Leibniz told to his friend and correspondent Des Bosses to imagine a circle, then to inscribe within it three congruent circles with maximum radius; the latter smaller circles could be filled with three even smaller circles by the same procedure. This process can be continued infinitely, from which arises a good idea of self-similarity. Leibniz's improvement of Euclid's axiom contains the same concept.
Scientist and engineer
Leibniz's writings are currently discussed, not only for their anticipations and possible discoveries not yet recognized, but as ways of advancing present knowledge. Much of his writing on physics is included in Gerhardt's Mathematical Writings.
Physics
See also:
dynamism (metaphysics)Leibniz contributed a fair amount to the statics and dynamics emerging about him, often disagreeing with
Descartes and
Newton. He devised a new theory of
motion (
dynamics) based on
kinetic energy and
potential energy, which posited space as relative, whereas Newton felt strongly space was absolute. An important example of Leibniz's mature physical thinking is his Specimen Dynamicum of 1695.
[27]Until the discovery of subatomic particles and the
quantum mechanics governing them, many of Leibniz's speculative ideas about aspects of nature not reducible to statics and dynamics made little sense. For instance, he anticipated
Albert Einstein by arguing, against Newton, that
space,
time and motion are relative, not absolute.
Leibniz's rule in interacting theories plays a role in
supersymmetry and in the lattices of
quantum mechanics. The
principle of sufficient reason has been invoked in recent
cosmology, and his
identity of indiscernibles in
quantum mechanics, a field some even credit him with having anticipated in some sense. Those who advocate
digital philosophy, a recent direction in cosmology, claim Leibniz as a precursor.
The vis viva
Leibniz's
vis viva (Latin for living force) is mv2, twice the modern
kinetic energy. He realized that the total energy would be conserved in certain mechanical systems, so he considered it an innate motive characteristic of matter.
[28] Here too his thinking gave rise to another regrettable nationalistic dispute. His vis viva was seen as rivaling the
conservation of momentum championed by Newton in England and by
Descartes in France; hence
academics in those countries tended to neglect Leibniz's idea.
Engineers eventually found vis viva useful, so that the two approaches eventually were seen as complementary.
[
edit] Other natural science
By proposing that the earth has a molten core, he anticipated modern
geology. In
embryology, he was a preformationist, but also proposed that organisms are the outcome of a combination of an infinite number of possible microstructures and of their powers. In the
life sciences and
paleontology, he revealed an amazing transformist intuition, fueled by his study of comparative anatomy and fossils. One of his principle works on this subject, Protogaea , unpublished in his lifetime, has recently been published in English for the first time. He worked out a primal organismic theory.
[29] In medicine, he exhorted the physicians of his time—with some results—to ground their theories in detailed comparative observations and verified experiments, and to distinguish firmly scientific and metaphysical points of view.
Social science
Technology
In 1906, Garland published a volume of Leibniz's writings bearing on his many practical inventions and engineering work. To date, few of these writings have been translated into English. Nevertheless, it is well understood that Leibniz was a serious inventor, engineer, and applied scientist, with great respect for practical life. Following the motto theoria cum praxis, he urged that theory be combined with practical application, and thus has been claimed as the father of
applied science. He designed wind-driven propellers and water pumps, mining machines to extract ore, hydraulic presses, lamps, submarines, clocks, etc. With
Denis Papin, he invented a
steam engine. He even proposed a method for desalinating water. From 1680 to 1685, he struggled to overcome the chronic flooding that afflicted the ducal
silver mines in the
Harz Mountains, but did not succeed.
[31][
edit] Information technology
Leibniz may have been the first computer scientist and information theorist.
[32] Early in life, he discovered the
binary number system (base 2), which is used on computers, then revisited that system throughout his career.
[33] He anticipated
Lagrangian interpolation and
algorithmic information theory. His
calculus ratiocinator anticipated aspects of the
universal Turing machine. In 1934,
Norbert Wiener claimed to have found in Leibniz's writings a mention of the concept of
feedback, central to Wiener's later
cybernetic theory.
In 1671, Leibniz began to invent a machine that could execute all four arithmetical operations, gradually improving it over a number of years. This "
Stepped Reckoner" attracted fair attention and was the basis of his election to the
Royal Society in 1673. A number of such machines were made during his years in
Hanover, by a craftsman working under Leibniz's supervision. It was not an unambiguous success because it did not fully mechanize the operation of carrying. Couturat reported finding an unpublished note by Leibniz, dated 1674, describing a machine capable of performing some algebraic operations.
[34]Leibniz was groping towards hardware and software concepts worked out much later by
Charles Babbage and
Ada Lovelace. In 1679, while mulling over his binary arithmetic, Leibniz imagined a machine in which binary numbers were represented by marbles, governed by a rudimentary sort of punched cards.
[35] Modern electronic digital computers replace Leibniz's marbles moving by gravity with shift registers, voltage gradients, and pulses of electrons, but otherwise they run roughly as Leibniz envisioned in 1679.
Librarian
While serving as librarian of the ducal libraries in
Hanover and
Wolfenbuettel, Leibniz effectively became one of the founders of
library science. The latter library was enormous for its day, as it contained more than 100,000 volumes, and Leibniz helped design a new building for it, believed to be the first building explicitly designed to be a library. He also designed a book
indexing system in ignorance of the only other such system then extant, that of the
Bodleian Library at
Oxford University. He also called on publishers to distribute abstracts of all new titles they produced each year, in a standard form that would facilitate indexing. He hoped that this abstracting project would eventually include everything printed from his day back to
Gutenberg. Neither proposal met with success at the time, but something like them became standard practice among English language publishers during the 20th century, under the aegis of the
Library of Congress and the
British Library.
He called for the creation of an
empirical database as a way to further all sciences. His
characteristica universalis,
calculus ratiocinator, and a "community of minds"—intended, among other things, to bring political and religious unity to Europe—can be seen as distant unwitting anticipations of artificial languages (e.g.,
Esperanto and its rivals),
symbolic logic, even the
World Wide Web.
Advocate of scientific societies
Leibniz emphasized that
research was a collaborative endeavor. Hence he warmly advocated the formation of national scientific societies along the lines of the British Royal Society and the French Academie Royale des Sciences. More specifically, in his correspondence and travels he urged the creation of such societies in Dresden, Saint Petersburg, Vienna, and Berlin. Only one such project came to fruition; in 1700, the
Berlin Academy of Sciences was created. Leibniz drew up its first statutes, and served as its first President for the remainder of his life. That Academy evolved into the German Academy of Sciences, the publisher of the ongoing critical edition of his works.
[36]Lawyer, moralist
No philosopher has ever had as much experience with practical affairs of state as Leibniz, except possibly
Marcus Aurelius. Leibniz's writings on law, ethics, and politics
[37] were long overlooked by English-speaking scholars, but this has changed of late.
[38]While Leibniz was no apologist for
absolute monarchy like
Hobbes, or for tyranny in any form, neither did he echo the political and constitutional views of his contemporary
John Locke, views invoked in support of democracy, in 18th-century America and later elsewhere. The following excerpt from a 1695 letter to Baron J. C. Boineburg's son Philipp is very revealing of Leibniz's political sentiments:
As for.. the great question of the power of sovereigns and the obedience their peoples owe them, I usually say that it would be good for princes to be persuaded that their people have the right to resist them, and for the people, on the other hand, to be persuaded to obey them passively. I am, however, quite of the opinion of
Grotius, that one ought to obey as a rule, the evil of revolution being greater beyond comparison than the evils causing it. Yet I recognize that a prince can go to such excess, and place the well-being of the state in such danger, that the obligation to endure ceases. This is most rare, however, and the theologian who authorizes violence under this pretext should take care against excess; excess being infinitely more dangerous than deficiency.
[39]In 1677, Leibniz called for a European confederation, governed by a council or senate, whose members would represent entire nations and would be free to vote their consciences;
[40] in doing so, he anticipated the
European Union. He believed that Europe would adopt a uniform religion. He reiterated these proposals in 1715.
Ecumenism
Leibniz devoted considerable intellectual and diplomatic effort to what would now be called
ecumenical endeavor, seeking to reconcile first the
Roman Catholic and
Lutheran churches, later the Lutheran and
Reformed churches. In this respect, he followed the example of his early patrons, Baron von Boineburg and the Duke
John Frederick—both cradle Lutherans who converted to Catholicism as adults—who did what they could to encourage the reunion of the two faiths, and who warmly welcomed such endeavors by others. (The House of
Brunswick remained Lutheran because the Duke's children did not follow their father.) These efforts included corresponding with the French bishop
Jacques-Bénigne Bossuet, and involved Leibniz in a fair bit of theological controversy. He evidently thought that the thoroughgoing application of reason would suffice to heal the breach caused by the
Reformation.
Philologist
Leibniz the
philologist was an avid student of languages, eagerly latching on to any information about
vocabulary and
grammar that came his way. He refuted the belief, widely held by Christian scholars in his day, that
Hebrew was the primeval language of the human race. He also refuted the argument, advanced by Swedish scholars in his day, that some sort of proto-
Swedish was the ancestor of the
Germanic languages. He puzzled over the origins of the
Slavic languages, was aware of the existence of
Sanskrit, and was fascinated by
classical Chinese.
Sinophile
Leibniz was perhaps the first major European intellect to take a close interest in
Chinese civilization, which he knew by corresponding with, and reading other work by, European Christian missionaries posted in China. He concluded that Europeans could learn much from the
Confucian ethical tradition. He mulled over the possibility that the
Chinese characters were an unwitting form of his
universal characteristic. He noted with fascination how the
I Ching hexagrams correspond to the
binary numbers from 0 to 111111, and concluded that this mapping was evidence of major Chinese accomplishments in the sort of philosophical mathematics he admired.
[41]As polymath
An episode from his life illustrates the breadth of Leibniz's genius. While making his grand tour of European archives to research the Brunswick family history that he never completed, Leibniz stopped in
Vienna between May 1688 and February 1689, where he did much legal and diplomatic work for the Brunswicks. He visited mines, talked with mine engineers, and tried to negotiate export contracts for lead from the ducal mines in the
Harz mountains. His proposal that the streets of Vienna be lit with lamps burning
rapeseed oil was implemented. During a formal audience with the
Austrian Emperor and in subsequent memoranda, he advocated reorganizing the Austrian economy, reforming the coinage of much of central Europe, negotiating a
Concordat between the
Habsburgs and the
Vatican, and creating an imperial research library, official archive, and public insurance fund. He wrote and published an important paper on
mechanics.
Leibniz also wrote a short paper, first published by
Louis Couturat in 1903,
[42] summarizing his views on
metaphysics. The paper is undated; that he wrote it while in Vienna was determined only in 1999, when the ongoing critical edition finally published Leibniz's philosophical writings for the period 1677–90. Couturat's reading of this paper was the launching point for much 20th-century thinking about Leibniz, especially among
analytic philosophers. But after a meticulous study of all of Leibniz's philosophical writings up to 1688—a study the 1999 additions to the critical edition made possible—Mercer (2001) begged to differ with Couturat's reading; the jury is still out.
When Leibniz died, his reputation was in decline. He was remembered for only one book, the
Théodicée, whose supposed central argument
Voltaire lampooned in his
Candide. Voltaire's depiction of Leibniz's ideas was so influential that many believed it to be an accurate description (this misapprehension may still be the case among certain lay people). Thus Voltaire and his Candide bear some of the blame for the lingering failure to appreciate and understand Leibniz's ideas. Leibniz had an ardent disciple,
Christian Wolff, whose dogmatic and facile outlook did Leibniz's reputation much harm. In any event, philosophical fashion was moving away from the rationalism and system building of the 17th century, of which Leibniz had been such an ardent exponent. His work on law, diplomacy, and history was seen as of ephemeral interest. The vastness and richness of his correspondence went unrecognized.
Much of Europe came to doubt that Leibniz had discovered the calculus independently of Newton, and hence his whole work in mathematics and physics was neglected. Voltaire, an admirer of Newton, also wrote Candide at least in part to discredit Leibniz's claim to having discovered the calculus and Leibniz's charge that Newton's theory of universal gravitation was incorrect. The rise of relativity and subsequent work in the history of mathematics has put Leibniz's stance in a more favorable light.
Leibniz's long march to his present glory began with the 1765 publication of the Nouveaux Essais, which
Kant read closely. In 1768, Dutens edited the first multi-volume edition of Leibniz's writings, followed in the 19th century by a number of editions, including those edited by Erdmann, Foucher de Careil, Gerhardt, Gerland, Klopp, and Mollat. Publication of Leibniz's correspondence with notables such as
Antoine Arnauld,
Samuel Clarke,
Sophia of Hanover, and her daughter
Sophia Charlotte of Hanover, began.
In 1900,
Bertrand Russell published a critical study of Leibniz's metaphysics. Shortly thereafter,
Louis Couturat published an important study of Leibniz, and edited a volume of Leibniz's heretofore unpublished writings, mainly on logic. While their conclusions, especially Russell's, were subsequently challenged and often dismissed, they made Leibniz somewhat respectable among 20th-century
analytical and
linguistic philosophers in the English-speaking world (Leibniz had already been of great influence to many Germans such as
Bernhard Riemann). For example, Leibniz's phrase
salva veritate, meaning interchangeability without loss of or compromising the truth, recurs in
Willard Quine's writings. Nevertheless, the secondary English-language literature on Leibniz did not really blossom until after World War II. This is especially true of English speaking countries; in
Gregory Brown's bibliography fewer than 30 of the English language entries were published before 1946. American Leibniz studies owe much to
Leroy Loemker (1904–85) through his translations and his interpretive essays in LeClerc (1973).
Nicholas Jolley has surmised that Leibniz's reputation as a philosopher is now perhaps higher than at any time since he was alive.
[43] Analytic and contemporary philosophy continue to invoke his notions of
identity,
individuation, and
possible worlds, while the doctrinaire contempt for
metaphysics, characteristic of analytic and linguistic philosophy, has faded. Work in the history of 17th- and 18th-century
ideas has revealed more clearly the 17th-century "Intellectual Revolution" that preceded the better-known
Industrial and commercial revolutions of the 18th and 19th centuries. The 17th- and 18th-century belief that natural science, especially physics, differs from philosophy mainly in degree and not in kind, is no longer dismissed out of hand. That modern science includes a "
scholastic" as well as a "radical
empiricist" element is more accepted now than in the early 20th century. Leibniz's thought is now seen as a major prolongation of the mighty endeavor begun by
Plato and
Aristotle: the universe and man's place in it are amenable to human
reason.
In 1985, the German government created the
Leibniz Prize, offering an annual award of 1.55 million
euros for experimental results and 770,000 euros for theoretical ones. It is the world's largest prize for scientific achievement.
Writings and edition
Leibniz mainly wrote in three languages: scholastic
Latin, French, and German. During his lifetime, he published many pamphlets and scholarly articles, but only two "philosophical" books, the Combinatorial Art and the
Théodicée. (He published numerous pamphlets, often anonymous, on behalf of the House of
Brunswick-Lüneburg, most notably the "De jure suprematum" a major consideration of the nature of
sovereignty.) One substantial book appeared posthumously, his
Nouveaux essais sur l'entendement humain, which Leibniz had withheld from publication after the death of
John Locke. Only in 1895, when Bodemann completed his catalogues of Leibniz's manuscripts and correspondence, did the enormous extent of Leibniz's
Nachlass become clear: about 15,000 letters to more than 1000 recipients plus more than 40,000 other items. Moreover, quite a few of these letters are of essay length. Much of his vast correspondence, especially the letters dated after 1685, remains unpublished, and much of what is published has been so only in recent decades. The amount, variety, and disorder of Leibniz's writings are a predictable result of a situation he described in a letter as follows:
I cannot tell you how extraordinarily distracted and spread out I am. I am trying to find various things in the archives; I look at old papers and hunt up unpublished documents. From these I hope to shed some light on the history of the [House of] Brunswick. I receive and answer a huge number of letters. At the same time, I have so many mathematical results, philosophical thoughts, and other literary innovations that should not be allowed to vanish that I often do not know where to begin.
[44]The extant parts of the critical edition
[45] of Leibniz's writings are organized as follows:
Series 1. Political, Historical, and General Correspondence. 21 vols., 1666–1701.
Series 2. Philosophical Correspondence. 1 vol., 1663–85.
Series 3. Mathematical, Scientific, and Technical Correspondence. 6 vols., 1672–96.
Series 4. Political Writings. 6 vols., 1667–98.
Series 5. Historical and Linguistic Writings. Inactive.
Series 6. Philosophical Writings. 7 vols., 1663–90, and
Nouveaux essais sur l'entendement humain.
Series 7. Mathematical Writings. 3 vols., 1672–76.
Series 8. Scientific, Medical, and Technical Writings. In preparation.
The systematic cataloguing of all of Leibniz's Nachlass began in 1901. It was hampered by two world wars, the NS dictatorship (with Jewish genocide, including an employee of the project, and other personal consequences), and decades of German division (two states with the cold war's "iron curtain" in between, separating scholars and also scattered portions of his literary estates). The ambitious project has had to deal with seven languages contained in some 200,000 pages of written and printed paper. In 1985 it was reorganized and included in a joint program of German federal and state (Länder) academies. Since then the branches in
Potsdam,
Münster,
Hannover and
Berlin have jointly published 25 volumes of the critical edition, with an average of 870 pages, and prepared index and
concordance works.
Selected works
The year given is usually that in which the work was completed, not of its eventual publication.
1666. De Arte Combinatoria (On the Art of Combination); partially translated in Loemker §1 and Parkinson (1966).
1671. Hypothesis Physica Nova (New Physical Hypothesis); Loemker §8.I (partial).
1673
Confessio philosophi (A Philosopher's Creed); an
English translation is available.
1684. Nova methodus pro maximis et minimis (New method for maximums and minimums); translated in Struik, D. J., 1969. A Source Book in Mathematics, 1200–1800. Harvard University Press: 271–81.
1686.
Discours de métaphysique; Martin and Brown (1988), Ariew and Garber 35, Loemker §35, Wiener III.3, Woolhouse and Francks 1. An
online translation by Jonathan Bennett is available.
1703. Explication de l'Arithmétique Binaire (Explanation of Binary Arithmetic); Gerhardt, Mathematical Writings VII.223. An
online translation by Lloyd Strickland is available.
1710.
Théodicée; Farrer, A.M., and Huggard, E.M., trans., 1985 (1952). Wiener III.11 (part). An
online translation is available at
Project Gutenberg.
1714.
Monadologie; translated by
Nicholas Rescher, 1991. The Monadology: An Edition for Students. University of Pittsburg Press. Ariew and Garber 213, Loemker §67, Wiener III.13, Woolhouse and Francks 19. Online translations:
Jonathan Bennett's translation;
Latta's translation;
French, Latin and Spanish edition, with facsimile of Leibniz's manuscript.1765.
Nouveaux essais sur l'entendement humain; completed in 1704. Remnant, Peter, and Bennett, Jonathan, trans., 1996. New Essays on Human Understanding. Cambridge University Press. Wiener III.6 (part). An
online translation by Jonathan Bennett is available.
CollectionsFour important collections of English translations are Wiener (1951), Loemker (1969), Ariew and Garber (1989), and Woolhouse and Francks (1998). The ongoing critical edition of all of Leibniz's writings is Sämtliche Schriften und Briefe.
[45]See alsoNewton v. Leibniz calculus controversyLeibniz-GemeinschaftLeibniz formulaLeibniz integral rule for differentiation under the integral sign
Leibniz testLeibniz harmonic triangleCitations
^ Baird, Forrest E.; Walter Kaufmann (2008). From Plato to Derrida. Upper Saddle River, New Jersey: Pearson Prentice Hall.
ISBN 0-13-158591-6.
^ Aiton 1985: 312
^ For a recent study of Leibniz's correspondence with Sophia Charlotte, see
MacDonald Ross (1998).
^ See Wiener IV.6 and Loemker § 40. Also see a curious passage titled "Leibniz's Philosophical Dream," first published by Bodemann in 1895 and translated on p. 253 of Morris, Mary, ed. and trans., 1934. Philosophical Writings. Dent & Sons Ltd.
^ Ariew & Garber, 69; Loemker, §§36, 38
^ Ariew & Garber, 138; Loemker, §47; Wiener, II.4
^ Ariew & Garber, 272–84; Loemker, §§14, 20, 21; Wiener, III.8
^ Mates (1986), chpts. 7.3, 9
^ Loemker 717
^ See Jolley (1995: 129–31), Woolhouse and Francks (1998), and Mercer (2001).
^ Loemker 311
^ For a precis of what Leibniz meant by these and other Principles, see Mercer (2001: 473–84). For a classic discussion of
Sufficient Reason and
Plenitude, see Lovejoy (1957).
^ Rutherford (1998) is a detailed scholarly study of Leibniz's
theodicy.
^ See
Ward & Brownlee (2000), Morris (2003: chpts. 5,6).
^ Barrow and Tipler (1986)
^ The Art of Discovery 1685, Wiener 51
^ Many of his memoranda are translated in Parkinson 1966.
^ Loemker, however, who translated some of Leibniz's works into English, said that the symbols of chemistry were real characters, so there is disagreement among Leibniz scholars on this point.
^ Preface to the General Science, 1677. Revision of Rutherford's translation in Jolley 1995: 234. Also Wiener I.4
^ A good introductory discussion of the "characteristic" is Jolley (1995: 226–40). An early, yet still classic, discussion of the "characteristic" and "calculus" is Couturat (1901: chpts. 3,4).
^ Struik (1969), 367
^ For an English translation of this paper, see Struik (1969: 271–84), who also translates parts of two other key papers by Leibniz on the calculus.
^ Hall (1980) gives a thorough scholarly discussion of the
calculus priority dispute.
^ Loemker §27
^ Mates (1986), 240
^ Mandelbrot (1977), 419. Quoted in Hirano (1997).
^ Ariew and Garber 117, Loemker §46, W II.5. On Leibniz and physics, see the chapter by Garber in Jolley (1995) and Wilson (1989).
^ See Ariew and Garber 155–86, Loemker §§53–55, W II.6–7a)
^ On Leibniz and biology, see Loemker (1969a: VIII).
^ On Leibniz and psychology, see Loemker (1969a: IX).
^ Aiton (1985), 107–114, 136
^ Davis (2000) discusses Leibniz's prophetic role in the emergence of calculating machines and of formal languages.
^ See Couturat (1901): 473–78.
^ Couturat (1901), 115
^ [1]^ On Leibniz’s projects for scientific societies, see Couturat (1901), App. IV.
^ See, for example, Ariew and Garber 19, 94, 111, 193; Riley 1988; Loemker §§2, 7, 20, 29, 44, 59, 62, 65; W I.1, IV.1–3
^ See (in order of difficulty) Jolley (2005: chpt. 7), Gregory Brown's chapter in Jolley (1995), Hostler (1975), and Riley (1996).
^ Loemker: 59, fn 16. Translation revised.
^ Loemker: 58, fn 9
^ On Leibniz, the I Ching, and binary numbers, see Aiton (1985: 245–48). Leibniz's writings on Chinese civilization are collected and translated in Cook and Rosemont (1994), and discussed in Perkins (2004).
^ Later translated as Loemker 267 and Woolhouse and Francks 30
^ Jolley, 217–19
^ 1695 letter to
Vincent Placcius in Gerhardt.
^
a b http://www.leibniz-edition.de/. See photograph there.

FIG. 2.4. Lower facial muscles in man. Right: superficial layers; Left: deep layers. (From Brausm 1954.)